Sorting is important in programming for the same reason it is important in real life.
It refers to arranging things in an order or manner and is helpful in tracking objects easily and quickly when desired. In other words, Sorting tends to make Searching less complicated.
Today, we are going to learn a not so new algorithm to sort objects, to be precise, numbers in this case. It's called Shell Sort.
Prerequisite
What is an algorithm?
An algorithm is a set of well defined computational steps which when followed accomplishes a given task.
It has the following features, which, in short, can be remembered as IODEF.
- I stands for Input. (minimum: 0)
- O stands for Output. (minimum: 1)
- D stands for Definiteness or Definitiveness
- E stands for Effectiveness
- F stands for Finiteness
Today, we are going to write the Shell Sort algorithm in C++ so it is important that the reader has understanding of its basic concepts before proceeding next.
"Insertion Sort as an underlying technique"
The Shell Sort algorithm contains implementation of Insertion Sort, so it is necessary that the reader has some prerequisite idea about the underlying algorithm first before moving further.
What is Insertion Sort?
Even though this blog basically covers Shell Sort and its implementation, in order to give readers a general idea/recollection of the algorithm Shell Sort is based on, I'll be recapping Insertion Sort in brief.
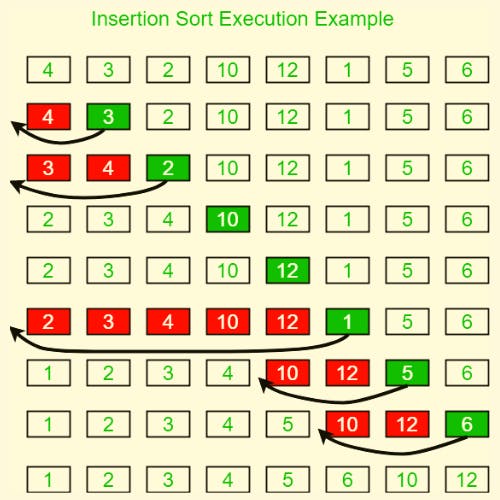
Insertion Sort is a simple sorting technique that follows the similar way in which we sort playing cards in our hands. Here, we take an array of numbers or values and virtually split it into two parts— sorted and unsorted.
Now follows a set of basic steps in which Insertion Sort works:
To sort an array of size n in ascending order, we do the below steps in the given order.
- First, we iterate from element at array index 0 to that in array index n-1 (or say n) over the array.
- While iterating, we select the current element as the key element.
- After iterating over the first array element, we compare the current element to the element preceding it.
- If the key element is smaller in value to its predecessor, we compare it to the element preceding the said predecessor.
- Again, if the key element is smaller, we compare it to the elements before, and the same goes on until the key element is no longer lesser in value compared to the element preceding it.
- Then, we move the greater elements up by one position to make space for the swapped key element.
Algorithm for Insertion Sort
insertionSort(array)
mark first element as sorted
for each unsorted element X
'extract' the element X
for j <- lastSortedIndex down to 0
if current element j > X
move sorted element to the right by 1
break loop and insert X here
end insertionSort
All about Shell Sort
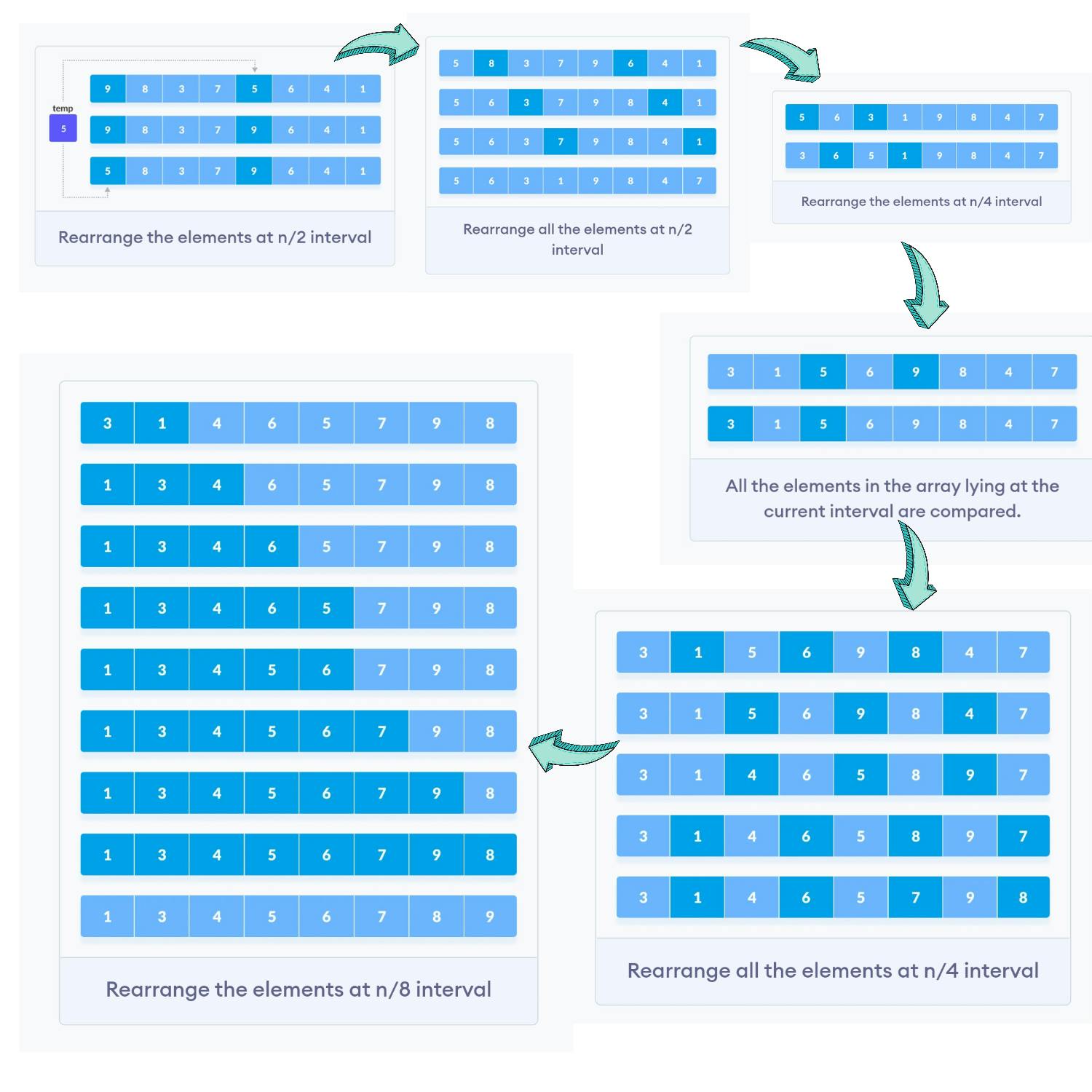
The Shell Sort algorithm can be best described as a generalized version of the Insertion Sort algorithm. It first sorts elements that are far apart from each other and then successively reduces the interval between the elements to be sorted.
Sequence
The interval between the elements is reduced based on the sequence used. Some of the sequences that can be used in the shell sort algorithm to optimize it are given below:
• Shell's Original Sequence:
N/2, N/4, N/8, ... , 1
• Knuth's Increments:
1, 4, 13, ... , (3k - 1)/2
• Sedgewick's Increments:
1, 8, 23, 77, 281, 1073, 4193, 16577, ... , 4^k - 3*2^k+ 1
• Hibbard's Increments:
1, 3, 7, 15, 31, 63, 127, 255, 511, ...
• Papernov & Stasevich Increments:
1, 3, 5, 9, 17, 33, 65, ...
• Pratt's Increments:
1, 2, 3, 4, 6, 9, 8, 12, 18, 27, 16, 24, 36, 54, 81, ...
In this blog, we will be taking Shell's Original Sequence as an example interval to understand the working of the algorithm.
Basic Steps
In order to sort an array of size n, we follow the basic steps provided below:
- We create an array of size n and accept elements into it.
Array Creation
int main() {
...
...
cout << "Enter array size: \n ";
cin >> n;
int Arr[n];
inputArray(Arr, n);
...
...
}
Array Initialization
void inputArray(int array[], int size) {
int i;
for (i = 0; i < size; i++)
{ cout << "Enter element " << i << ": ";
cin >> array[i];
}
}
- An interval (here, Shell's Original Sequence) is decided on the basis of which the array will be divided.
- We initialize the value of the interval h and then divide the array into smaller sub-array of equal interval h.
- We sort these smaller sub-arrays using the underlying algorithm of Insertion Sort.
- This process is repeated until we are left with all the elements in the array sorted.
// Implementation of Insertion Sort
void shellSort(int array[], int n) {
// Rearrange elements at each n/2, n/4, n/8, ... intervals
for (int interval = n / 2; interval > 0; interval /= 2) {
for (int i = interval; i < n; i += 1) {
int temp = array[i];
int j;
for (j = i; j >= interval && array[j - interval] > temp; j -= interval) {
array[j] = array[j - interval];
}
array[j] = temp;
}
}
}
- Then we print the array.
void printArray(int array[], int size) {
int i;
for (i = 0; i < size; i++)
cout << array[i] << " ";
cout << endl;
}
Algorithm
Below given is an algorithm derived from the basic steps:
shellSort(array, size)
for interval i <- size/2n down to 1
for each interval "i" in array
sort all the elements at interval "i"
end shellSort
or
ShellSort(a, n) // 'a' is the given array, 'n' is the size of array
for (interval = n/2; interval > 0; interval /= 2)
for ( i = interval; i < n; i += 1)
temp = a[i];
for ( j = i; j >= interval && a[j - interval] > temp; j -= interval)
a[j] = a[j - interval];
a[j] = temp;
End ShellSort
The whole code to implement Shell Sort can be found below for reader's reference and understanding, which consists of options for both Sample Input and User Desired Input:
// Shell Sort in C++ programming
// Using Shell's original sequence as intervals in the algorithm
#include <iostream>
using namespace std;
// Shell sort
void shellSort(int array[], int n) {
// Rearrange elements at each n/2, n/4, n/8, ... intervals
for (int interval = n / 2; interval > 0; interval /= 2) {
for (int i = interval; i < n; i += 1) {
int temp = array[i];
int j;
for (j = i; j >= interval && array[j - interval] > temp; j -= interval) {
array[j] = array[j - interval];
}
array[j] = temp;
}
}
}
// Print an array
void printArray(int array[], int size) {
int i;
for (i = 0; i < size; i++)
cout << array[i] << " ";
cout << endl;
}
// Input elements into array
void inputArray(int array[], int size) {
int i;
for (i = 0; i < size; i++)
{
cout << "Enter element " << i << ": ";
cin >> array[i];
}
}
// Driver code
int main() {
int data[] = {9, 8, 3, 7, 5, 6, 4, 1};
int size = sizeof(data) / sizeof(data[0]);
cout << "For Sample Array: " << endl << "..................... " << endl;
cout << "Unsorted Array: \n";
printArray(data, size);
shellSort(data, size);
cout << "Sorted array: \n";
printArray(data, size);
int n;
cout << "For User Input Array: " << endl << "..................... " << endl;
cout << "Enter array size: \n ";
cin >> n;
int Arr[n];
inputArray(Arr, n);
cout << "Unsorted Array: \n";
printArray(Arr, n);
shellSort(Arr, n);
cout << "Sorted array: \n";
printArray(Arr, n);
}
Sample input and output for the given program can be found below:
/* Sample Output
For Sample Array:
.....................
Unsorted Array:
9 8 3 7 5 6 4 1
Sorted array:
1 3 4 5 6 7 8 9
For User Input Array:
.....................
Enter array size:
7
Enter element 0: 12
Enter element 1: 56
Enter element 2: 98
Enter element 3: 22
Enter element 4: 5
Enter element 5: 3
Enter element 6: 10
Unsorted Array:
12 56 98 22 5 3 10
Sorted array:
3 5 10 12 22 56 98
*/
Let's move on to the properties of Shell Sort to see when and why this algorithm is preferred (or not).
Properties
• Time Complexity: It can be referred to as the computational complexity that describes the amount of time taken by a machine (computer) to run an algorithm. It usually includes both compilation as well as execution time, but the compilation time is very small as compared to run time, hence it is neglected.
Best Case Complexity:
O(n*logn)occurs when there is no sorting required, i.e., the array is already sorted. The best-case time complexity of Shell Sort is O(n*logn).
Average Case Complexity:
O(n*logn)occurs when the array elements are in jumbled order that is not properly ascending and not properly descending. The average-case time complexity of Shell Sort is O(n*logn).
Worst Case Complexity:
O(n^2)occurs when the array elements are required to be sorted in reverse order. That means suppose you have to sort the array elements in ascending order, but its elements are in descending order. The worst-case time complexity of Shell Sort is O(n^2). According to Poonen Theorem, worst case complexity for shell sort is
O(Nlog N)^2/(log log N)^2)orO(Nlog N)^2/log log N)orO(N*(log N)^2)or something in between.
• Space Complexity: It is referred to as the total amount of memory space utilised by the computer to store an algorithm or program, including the space for input values. The complexity is significantly determined by the number of inputs provided.
- Shell Sort Space Complexity:
O(1)
• Stability: It plays an important role when duplicate values come into play. Stability is said to be maintained when two duplicate or equivalent values retain their relative positions after the sorting is completed.
- Is Shell Sort stable?
No
• In-place: It means the algorithm does not use extra space for manipulating the input but may require a small though non-constant extra space for its operation.
- Is Shell Sort in-place?
Yes
Advantages
Shell Sort is preferred when:
• Calling a stack is overhead. uClibc library uses this sort.
• Recursion exceeds a limit. bzip2 compressor uses it.
• Insertion Sort does not perform well when the close elements are placed too far apart. Shell Sort helps in reducing the distance between those elements, resulting in less number of times of swapping to be performed.
• Shell Sort algorithm is 5.32 times faster than the Bubble Sort algorithm.
Disadvantages
Let's talk about some disadvantages of Shell Sort.
It has the following disadvantages:
• Shell Sort algorithm is complex in structure and bit more difficult to understand without understanding the underlying algorithm first.
• Shell Sort algorithm is significantly slower than the Merge Sort, Quick Sort and Heap Sort Algorithms.

